LogServiceで扱える機械学習の時系列分析を使ってみました ~単一時系列処理編~
LogServiceで扱える機械学習の時系列分析を使ってみました ~単一時系列処理編~
はじめに
本記事では、LogServiceで扱える機械学習の時系列分析についてをご紹介します。
今回は、初めの一歩としてLogServiceで使用することのできる時系列分析の機械学習を全てではありませんが、私が一通り使用した中で有用だと感じた関数に関して、どのようなデータに対して有効であるか説明します。
今回のブログでは単一時系列の処理のみを紹介していこうと思います。また、前提といたしまして国際サイトのLogServiceを使用しております。
用意したデータについて
LogServiceで行える時系列処理のほとんどが単一時系列(ある時間に対しデータが1つ)の処理となっています。
今回は、以下の3種類の異なる傾向のデータを作成し、それぞれのアルゴリズムによって処理結果がどう変化するかを比較しながら解説していきます。
また、それぞれのデータは140プロットであり、異常値を少しだけ組み込んでいます。
データA: 不定期に値が上昇するデータ
データB: 周期性のあるデータ
データC: 周期性のない緩やかなデータ
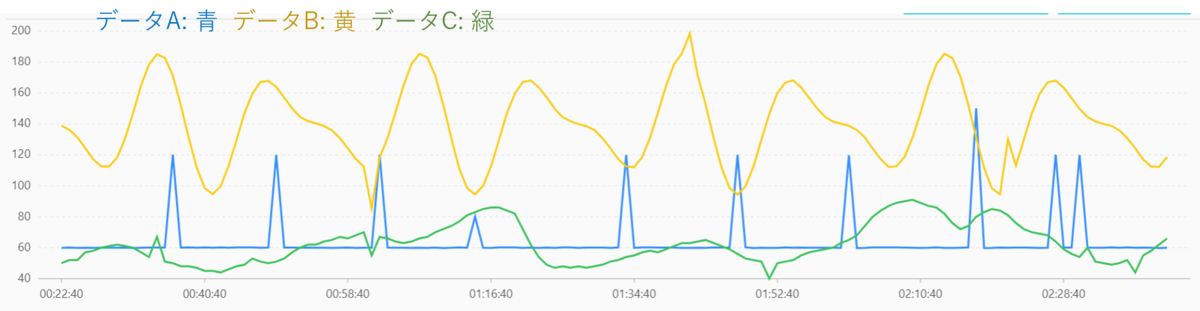
データに関しては、Excelの関数を用いたり、手動で入力したりして作成しています。
データ投入は、Pythonを用いてAPI経由で投入しています。
単一時系列に対する操作
単一時系列に対する操作では以下のことが主に行えます。
- ・データの平滑化
- ・周期の推定
- ・変化点検出
- ・最大値検出
- ・異常検出および予測
- ・シーケンス分解
データの平滑化
データを平滑化します。
ノイズが多いセンサなどの前処理として使うことになります。使用できるクエリの関数は、
- ・ts_smooth_simple
- ・ts_smooth_fir
- ・ts_smooth_iir
があります。今回は上の2つを紹介していきます。
ts_smooth_simple
Holt Winters と呼ばれるアルゴリズムでデータを平滑化します。
このアルゴリズムの前提として、明確な季節変動 (一定の周期変動)のある時系列データのみ扱えます。
今回用意したデータの場合だと、 データBしか扱うことができません。
* | select ts_smooth_simple(timestamp, value)
- ・timestamp : タイムスタンプ
- ・value : 値
引数は、タイムスタンプと値しか必要としません。
結果は以下のようになります。
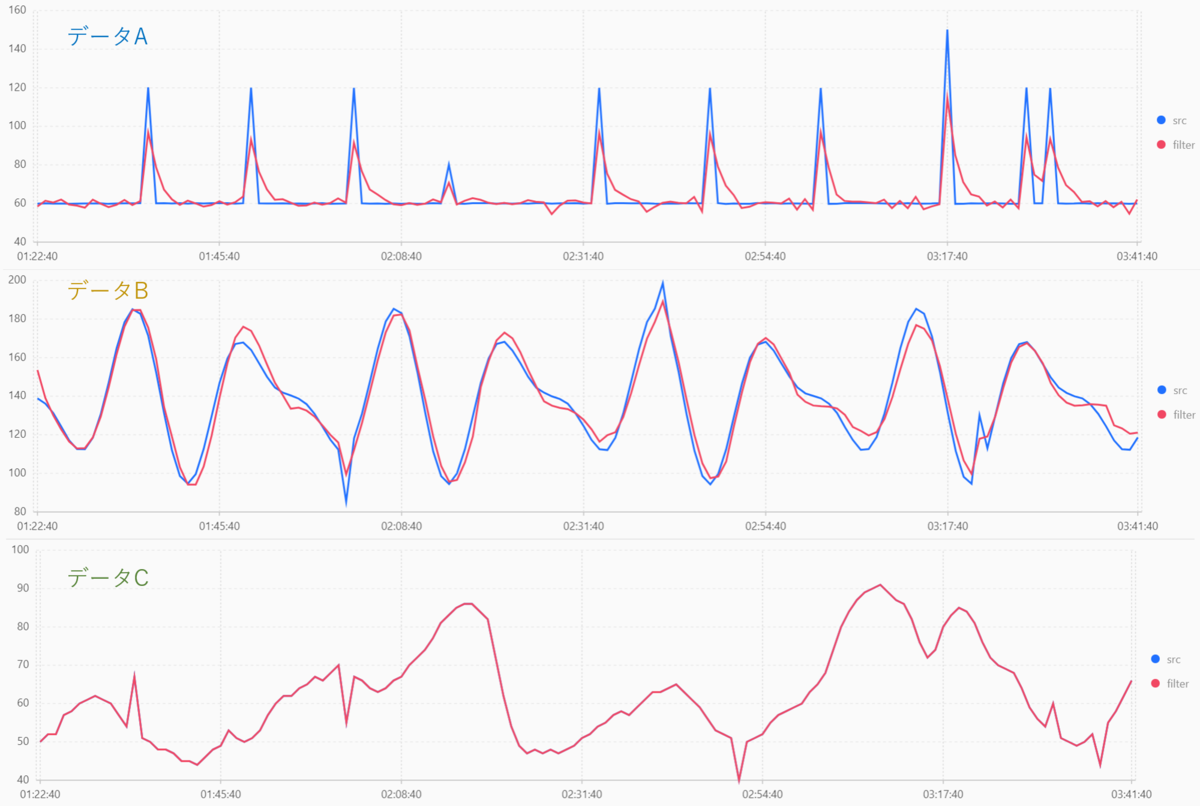
データC は全く変わっていませんし、データA に関しては逆効果のように見えますね。
ts_smooth_fir
FIRフィルターを使用して時系列データを平滑化します。
FIRフィルタとは、 日本語では有限インパルス応答フィルタと呼ばれ、有限個のデータをもとにフィルタリングしていく方式です。
簡単に言いますと、フィルタ対象のプロットの周囲何個かのデータのみを用いて値を求めます。
一方、今回紹介はしない ts_smooth_iir は、IIR(無限インパルス応答)フィルタと呼ばれる手法を用いており、無限個のデータでフィルタリングします。
簡単に言いますと、FIRフィルタのようにフィルタ対象のプロットの周囲何個かのデータのみを用いて値を求めた結果に加えて、前の何個かのプロットの結果をフィードバックし値を求める方式です。前の結果のフィードバックを入れるので、1プロット目のデータでもNプロット目の結果に影響を与えるので無限個となります。
今回用意したデータでは、ほとんどFIRフィルターと変わらなかったため本ブログでは紹介しないこととします。
* | select ts_smooth_fir(timestamp, value, winType, winSize, samplePeriod, sampleMethod)
- ・winTipe : フィルターウインドウタイプ
- ・winSize : ウインドウサイズ
- ・samplePeriod : サンプリング間隔 (省略可)
- ・sampleMethod : サンプリング手法 (省略可)
フィルターウインドウタイプに関しては、以下の4種類あります。
- ・rectangle : 矩形窓
- ・hanning : ハン窓(ハニング窓)
- ・hamming : ハミング窓
- ・blackman : ブラックマン窓
以上のタイプのうち、rectangle だけ大きく傾向が異なっており、対象のプロットを中心とした周りのデータの平均をとって平滑化します。
それ以外の3種類は、対象のプロットを中心とした周りのデータに比重を掛け合計し平滑化します。このとき、対象のプロットが一番比重が高く、離れていくにつれて小さくなっていきます。この3種類は比重の計算式が異なっているだけとなります。
それぞれの窓関数の形と計算式は省略します。
ウインドウサイズは、何個のデータで平滑化するかの指定となります。
例えば 5 を指定した場合は、対象のプロットと、未来と過去の2プロットずつを用いて平滑化します。
使ってみた結果ですが、偶数を指定した場合は過去が多くなるようです。例えば 4 を指定した場合は、対象のプロットと未来1,過去2プロットとなります。
またこの時の比重ですが対象のプロットと1つ過去のプロットは同じ比重となっていました。
winTipe=hamming, winSize=7 としたときの結果は以下のようになります。
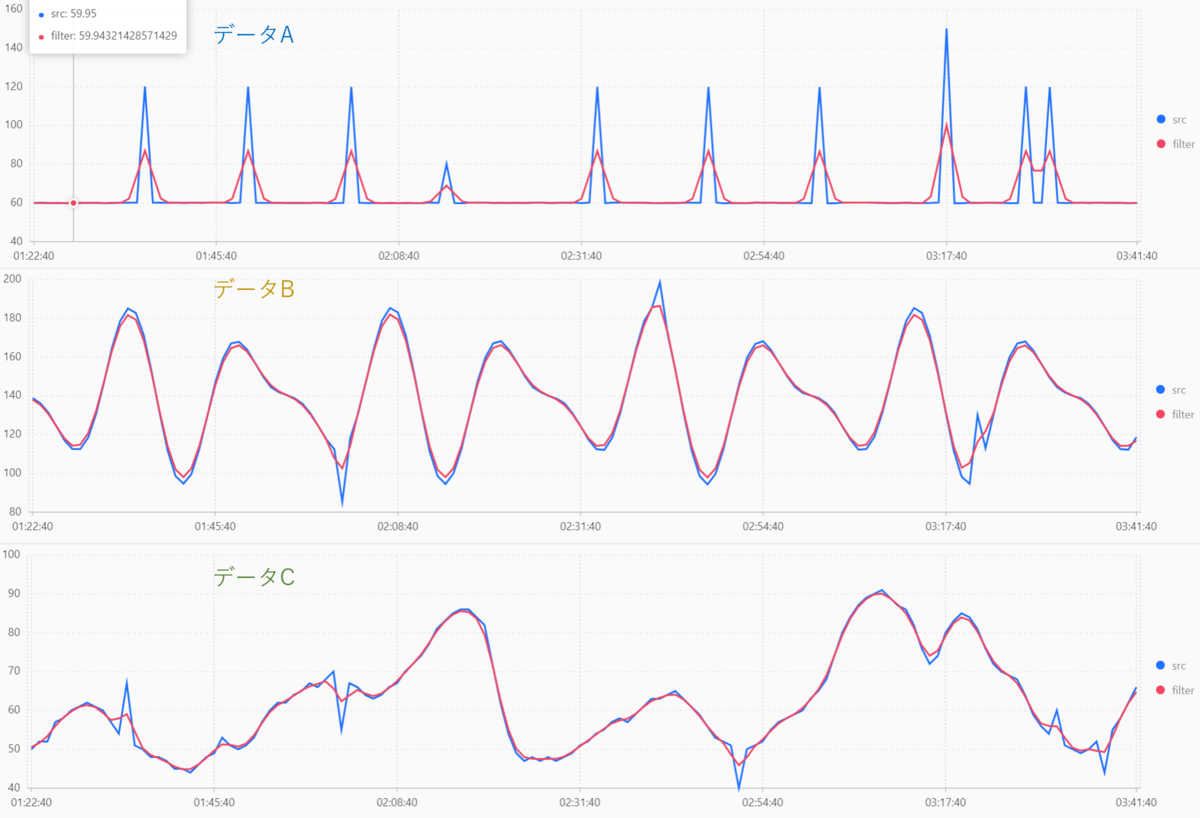
どのデータでも平滑化がうまくできましたね。
ただ、winSizeを大きくするとデータによっては異常値として捉えたい個所まで消えてしまう可能性があるので、前処理として用いる際にはパラメータ設定に注意しましょう。
また、任意の比重で平滑化することも可能となっています。
* | select ts_smooth_fir(timestamp, value, array[], samplePeriod, sampleMethod)
配列の中身は double型で、合計を必ず 1.0 にしなければなりません。
array[0.1,0.2,0.4,0.15,0.15] とした場合、対象のプロットは0.4, 過去2プロットが0.15ずつ未来のプロットが0.2と0.1のようになります。
周期の推定
全時間の中から、周期を抽出するアルゴリズムです。
関数は、 ts_period_detect のみとなっています。
ts_period_detect
* | select ts_period_detect(timestamp, value, minPeriod, maxPeriod, samplePeriod, sampleMethod)
- ・minPeriod : 全期間に対する周期の長さの比率の最低値
- ・maxPeriod : 全期間に対する周期の長さの比率の最大値
例えば、1000プロットのデータがある場合に、minPeriod=0.1,maxPeriod=0.3 のように入力した場合は、
100プロットから300プロットで構成される周期を抽出します。
結果は以下のようになります。
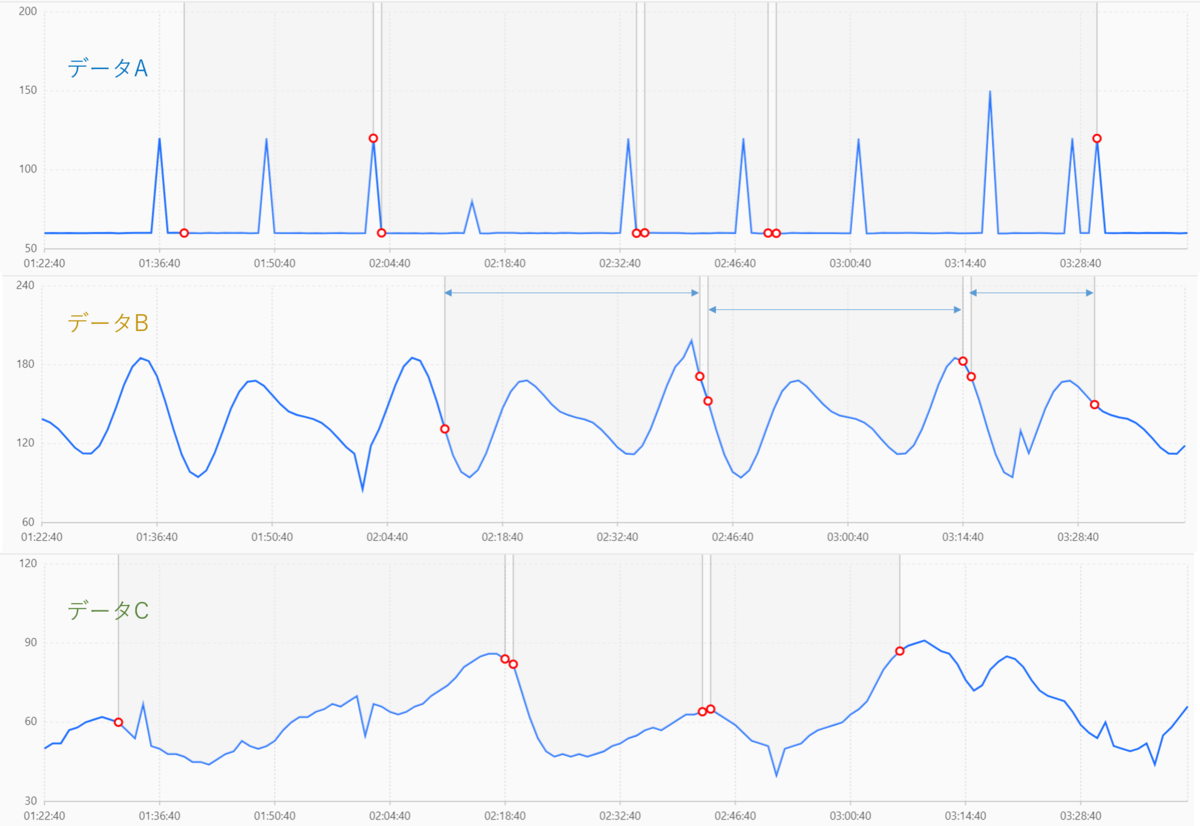
グラフの見方としては、赤丸は2つでワンセットとなっておりそれぞれ開始と終了を示しています。 (データBの結果に参考用に矢印をつけています。)
注意点として、このクエリの結果は1カラム内に配列で出力されます。
形式的には以下の形です。
[[タイムスタンプの配列],[値の配列],[期間推定結果]]
文字だと少しわかりずらいですね。
今回の データB の結果を見るとこのようになっていました。
[[1580574160.0,1580574220.0,1580574280.0,1580574340.0,1580574400.0・・・], [171.5579261,173.4778335,175.288474,176.9803017,178.5442326・・・], [1.0,0.0,0.0,0.0,0.0・・・]]
なかなかに扱い方が難しそうです。。。
また、今回用意した3種のデータは周期が少なすぎたので、データBのプロット数を増やした別のデータでも試してみました。
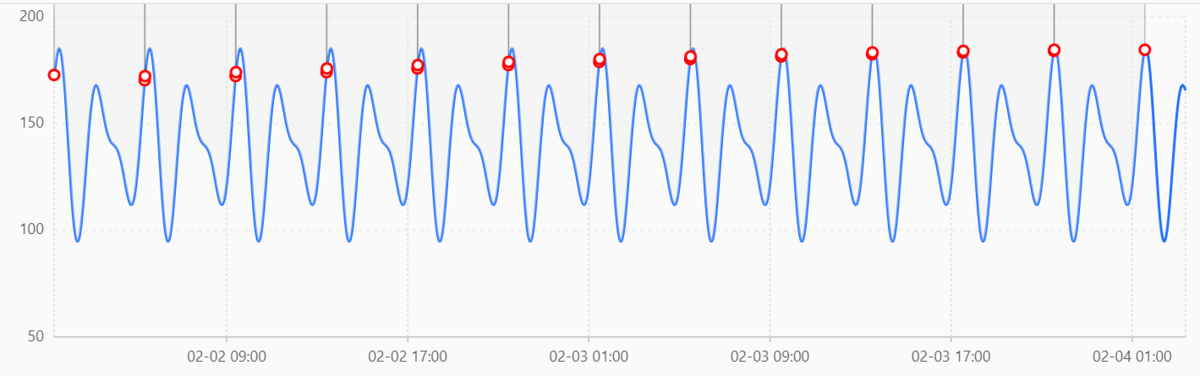
若干ずれていますが、ちゃんと周期がとれていそうですね。
変化点検出
全期間の中から、データの傾向が変化した点を抽出します。
クエリの関数は以下の2つが使用できます。
- ・ts_cp_detect
- ・ts_breakout_detect
ts_cp_detect
指定期間内の統計的特性の変化を見つけ変化点を抽出します。
* | select ts_cp_detect(timestamp, value, minSize, samplePeriod, sampleMethod)
- ・minSize : 間隔の最小値(何個のデータで特性をみるか)
具体的なアルゴリズムの内容は記載されていないので詳細はわかりませんが、前後のウィンドウで傾向に大きな差があれば、変化点とするようです。
minSize=3 の時の結果は以下のようになります。
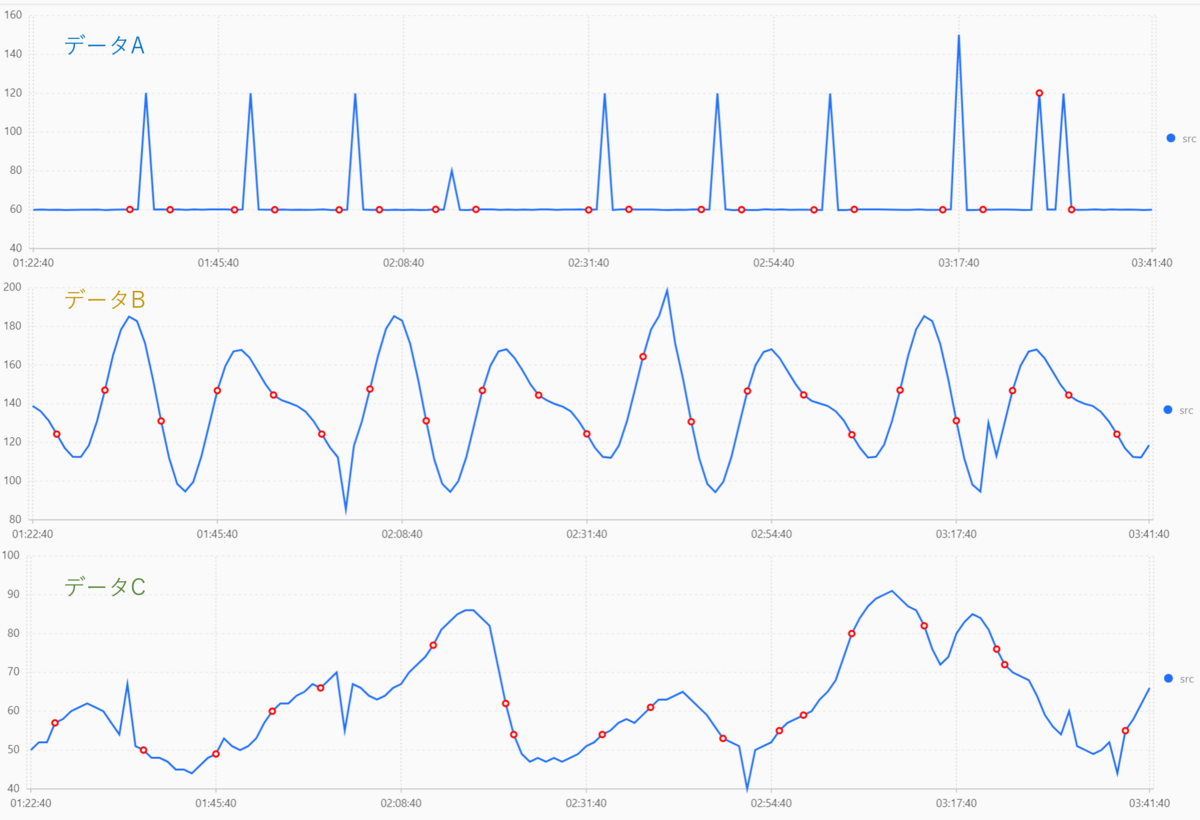
赤丸が変化点とみなした個所になります。
データA は良いデータが取れていますが、 データB と データC に関しては変化点だらけですね。
下の結果は、データB のデータ量を増やし、 minSizeを周期に近づさせた場合の結果です。
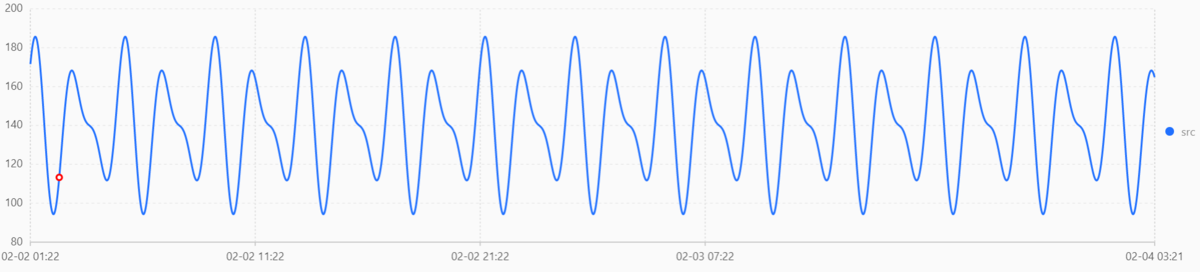
1か所だけ出てしまいましたが、ほとんど変化点がなくなりましたね。

変化がある場合にはきちんと検出してくれます。
定常性のあるデータか、1周期の間隔がある程度決まっている周期データであれば良い検出ができそうですね。 それ以外のデータではあまり有用性が見らなさそうです。ts_breakout_detect
時系列内で統計が急激に増加または減少する時点を見つけるための関数です。
* | select ts_breakout_detect(timestamp, value, minSize, samplePeriod, sampleMethod)
結果は以下のようになります。
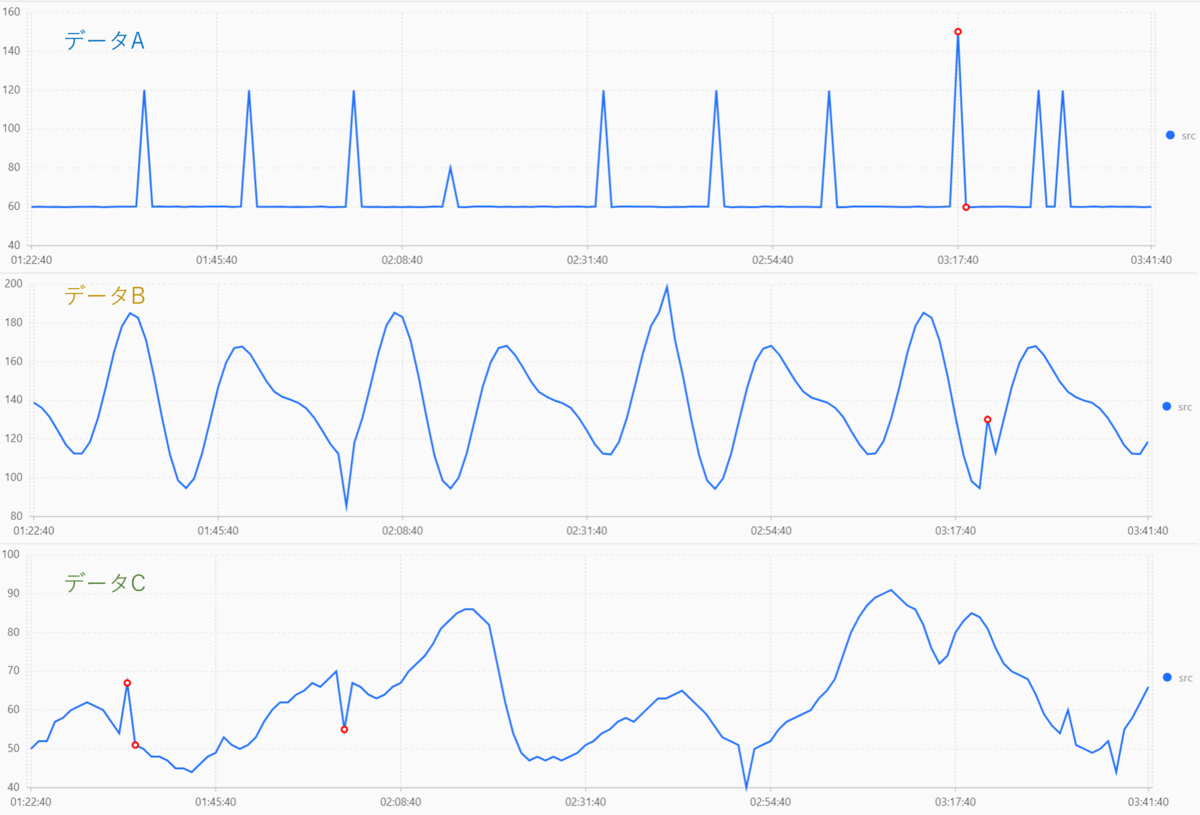
データA の結果を見ると確認出来ますが、単純に前後で大きく変化した場所を見るのではなく、時系列全体的に見て大きく増加・減少している点を見つけてくれます。
主な用途としては、外れ値の検知に利用できそうですね。
最大値検出
シーケンス内の最大値を検出します。
クエリの関数は、 ts_find_peaks のみです。
ts_find_peaks
* | select ts_find_peaks(timestamp, value, minSize, samplePeriod, sampleMethod)
赤丸が検出した最大値となります。
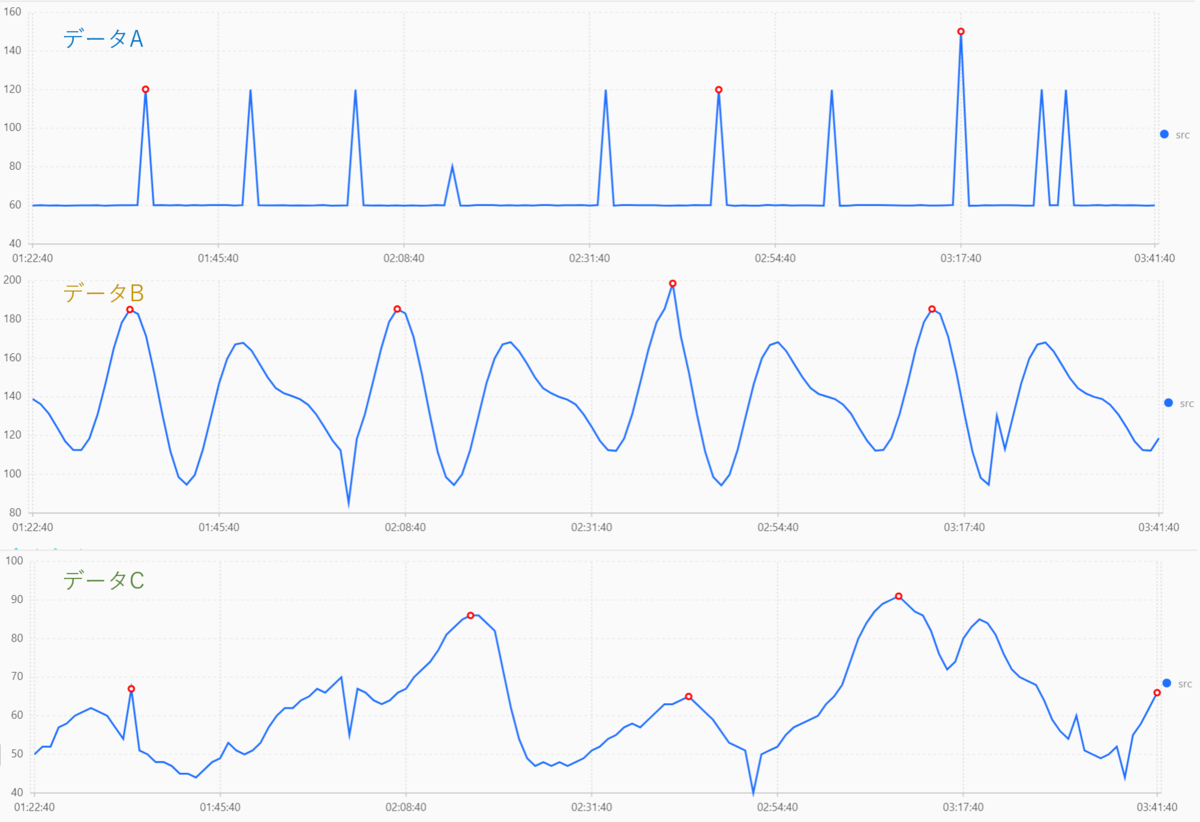
データA の結果は少し微妙でしたが、データBとデータCに関しては検出できていそうです。
この関数単体では最大値検出するだけですので、実運用時には何かしらの後処理が必要になりますね。
最大値だけではありますが、緩やかに上昇した場合等でも捉えてくれるので、後処理次第ですが変化点検出や次に紹介する異常検出等で引っかからない故障データも検知可能であると考えられます。
具体的な後処理としてできそうなのは、 PAIにMaxCompute経由等でデータ連携させてクラスタリングや分類をするといったことが考えられますね。
また残念ながら、最小値検出は現在ありません。必要な場合は値を反転させて検出するしかないですね。
異常検出および予測
異常検出および予測を行うことができます。
クエリの関数は、
- ・ts_predicate_simple
- ・ts_predicate_ar
- ・ts_predicate_arma
- ・ts_predicate_arima
が存在します。
冒頭に紹介した石井さんのブログにも書かれていますので、そちらもご確認ください。
ts_predicate_simple
あらかじめ用意されているパラメータで時系列予測と異常検知を行います。
* | select ts_predicate_simple(timestamp, value, nPred, isSmooth, samplePeriod, sampleMethod)
- ・nPred : 予測するプロット数
- ・isSmooth : 平滑化するかどうか (boolean) defalt: true
結果は以下のようになります。
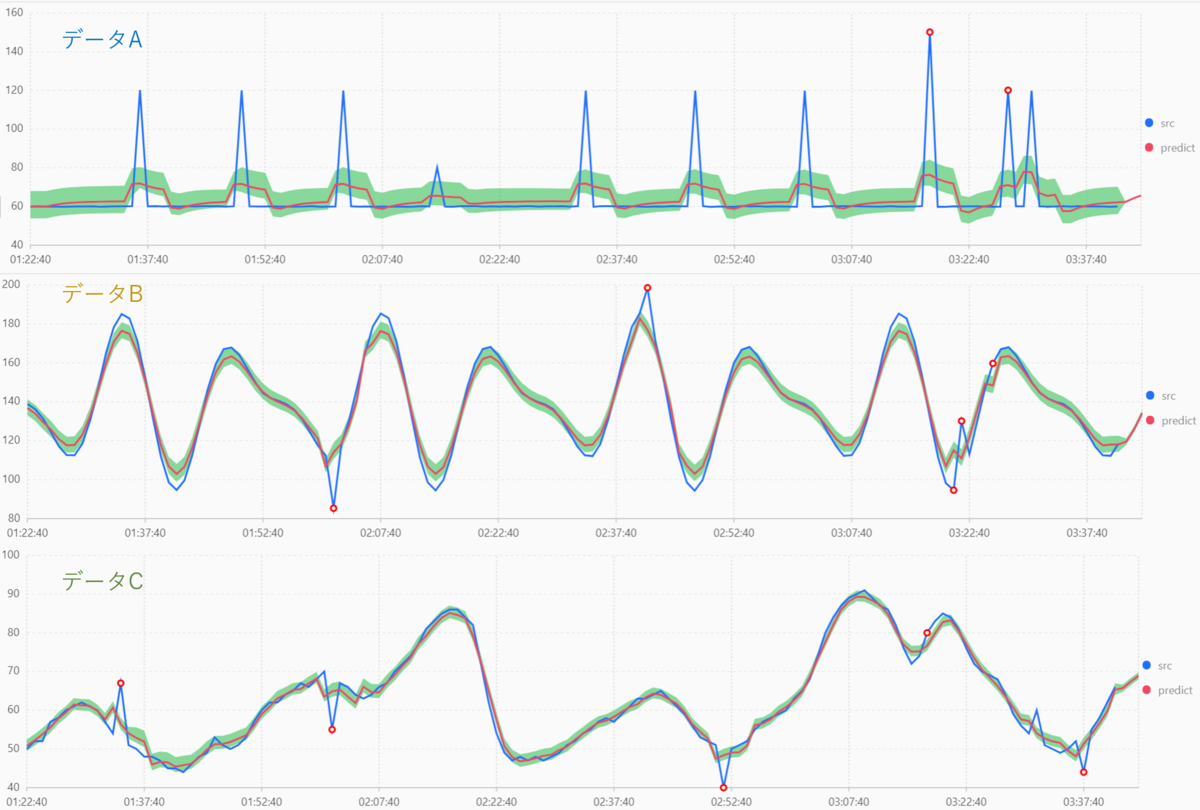
青色が元のデータで、赤色が予測データになります。
緑色の範囲は、信頼水準85%の信頼区間と呼ばれるものですが、予測の上限と下限の範囲くらいの認識で問題ないです(厳密には違いますが)。
そして、赤丸が異常とみなした部分になります。
しかしながら、結果を見るとこの緑色の範囲から外れているにも関わらず、異常とみなされていない部分がたくさんありますね。
中国サイトの ブログ を読む限りだと、LogServiceでの異常検出は内部的にたくさんの戦略を採用しているそうです。
データAの結果を見ると、値が 120 に増加している部分はおおむね正常値として捉えていて、80 と 140 への増加は異常とみなしていますね。 何かしら別のアルゴリズムが働いていると考えられます。
ts_predicate_ar
自己回帰モデル(ARモデル)と呼ばれる手法を用いて、時系列予測と異常検知を行います。
アルゴリズムの詳細については簡単に紹介できないため省略させていただきます。
* | select ts_predicate_ar(timestamp, value, p, nPred, isSmooth, samplePeriod, sampleMethod)
- ・p : いくつ前までのデータを用いて自己回帰するか。
ちなみにこのパラメータの範囲ですが、 [2, 100] です。
また、合計プロット数の半分以上の値は設定不可能となっています。 (140プロットなら 2 <= p <= 70)
データの見方は、 ts_predicate_simple と同じです。
使ってみた結果はこちらになります。
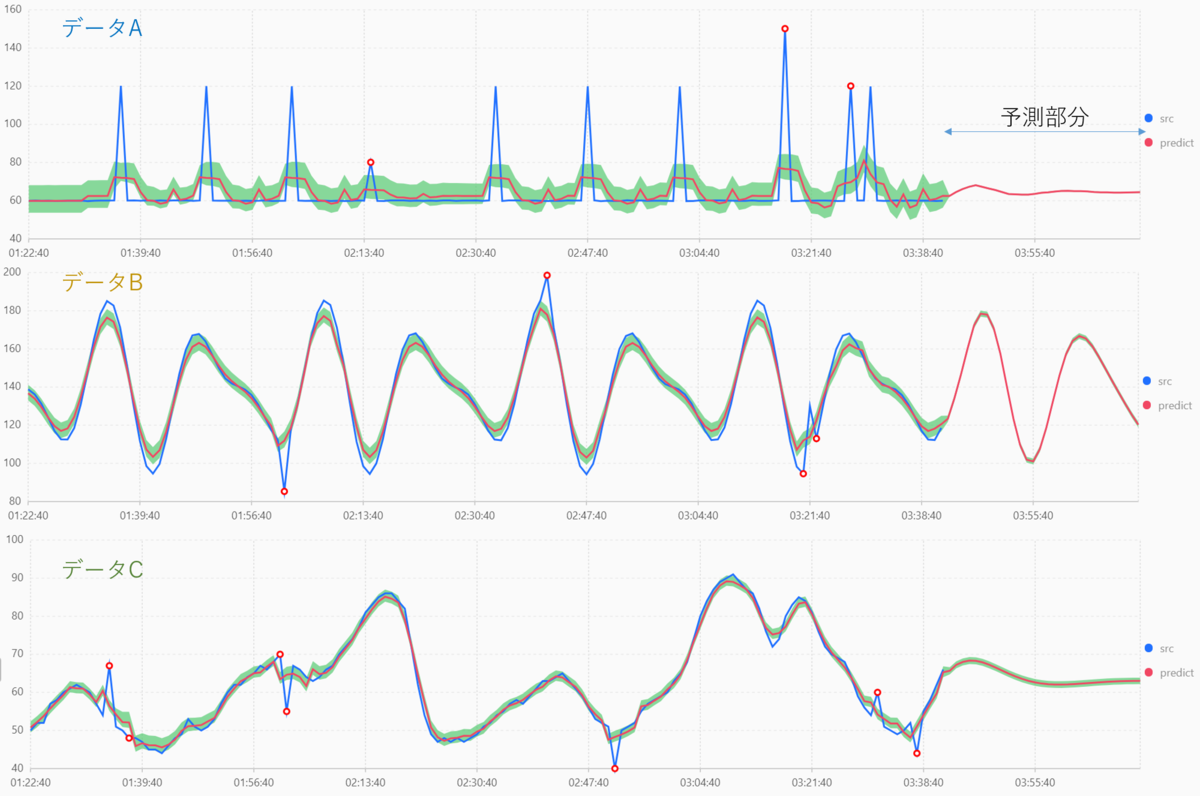
結構いい感じに検知できていますね。
ちなみに、青い線がなく、赤い線しかない時間帯がありますが、これは予測した結果となっています。
クエリを発行する際は、 nPred で指定した数だけ limit の値を増加させましょう。
ts_predicate_arma と ts_predicate_arima
この2つは、ts_predicate_ar と似ているので結果は割愛いたします。
それぞれ、 自己回帰移動平均(ARMA)モデル と 自己回帰統合移動平均(ARIMA)モデル と呼ばれる手法を用いています。
* | select ts_predicate_arma(timestamp, value, p, q, nPred, isSmooth, samplePeriod, sampleMethod)
* | select ts_predicate_arima(timestamp, value, p, d, q, nPred, isSmooth, samplePeriod, sampleMethod)
q の値の範囲は [2, 100] で、d は [1, 3] です。
シーケンス分解
時系列データを分析し、 trend (傾向)、season (季節性,周期性) 、residual (残差) を求めます。
使用できる関数は、 ts_decompose のみとなります。
ts_decompose
trend (傾向)は、長期的に見て上昇・下降しているなどの傾向を調べるのに適しています。
season (季節性,周期性)は、どのような周期性があるのかを調べるのに適しています。
residual (残差) は、上記2種に含まれない情報であり、短期的な不規則変化(ノイズ)を主に表しています。
* | select ts_decompose(timestamp, value, samplePeriod, sampleMethod)
結果は以下のようになります。
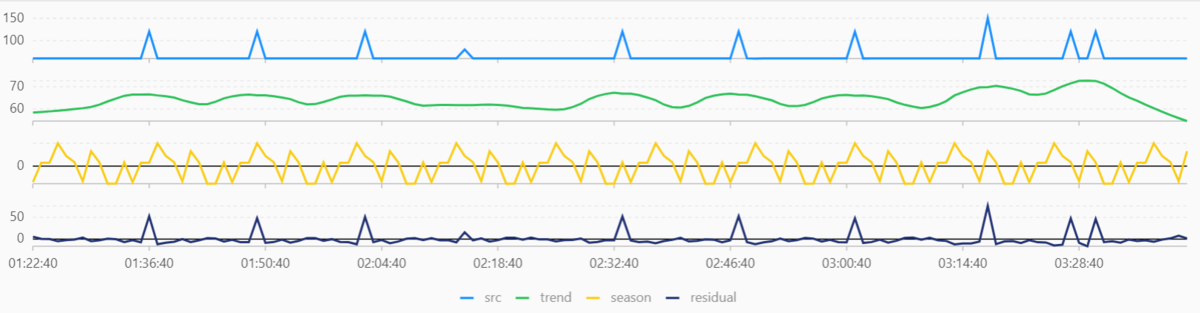
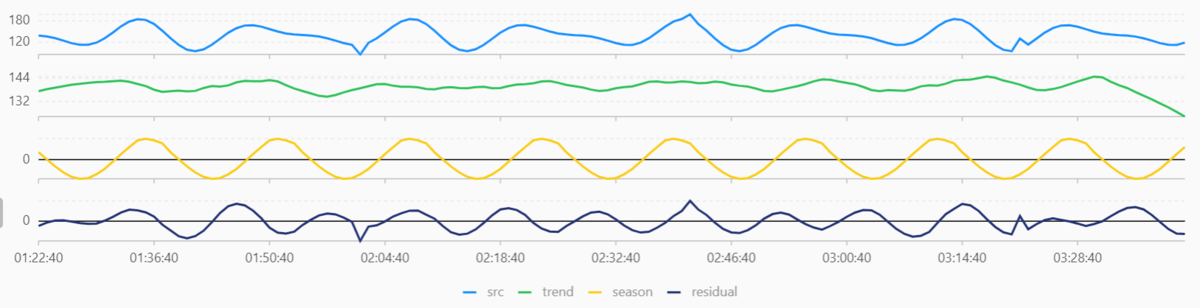
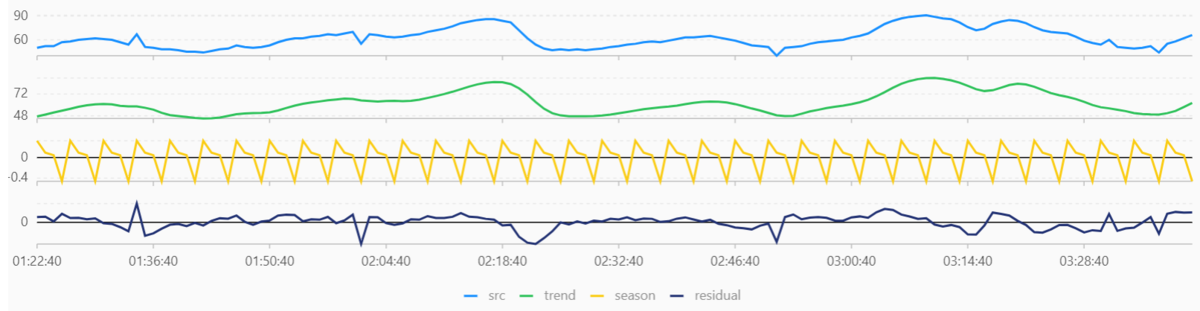
データAのような定常値がはっきりしているうえに短期的にしか変化しない時系列データに関しては、この関数の使いどころはなさそうですね。
データBに関しては、trend で長期的には 約140 で一定なデータであることが読み取れます。season からもきれいな周期性を持っていることが読み取れますね。データBを作成する際に、Excelで140を中心にsinとcosを組み合わせて作成しているのでだいたいあっています。
データCは、 trend からデータの傾向がしっかり読み取れますし、residual で短期間で大きく変動した所を読み取ることができます。
また、今回はデータBのプロット数を増やし、上昇と下降を付与したデータも用意しました。
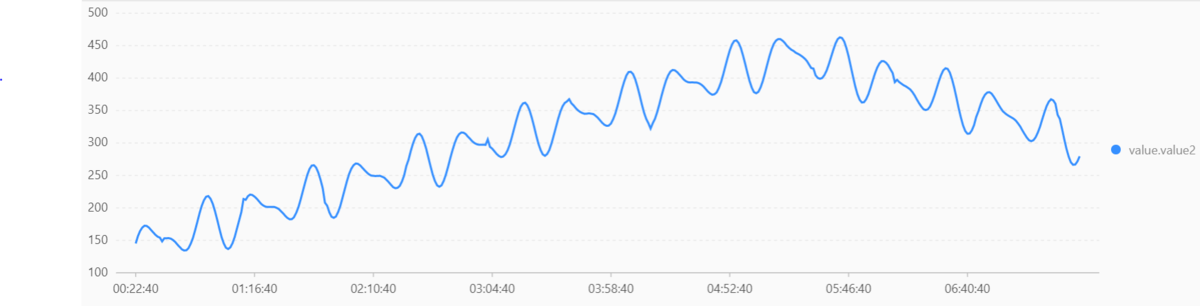
結果は以下のようになります。
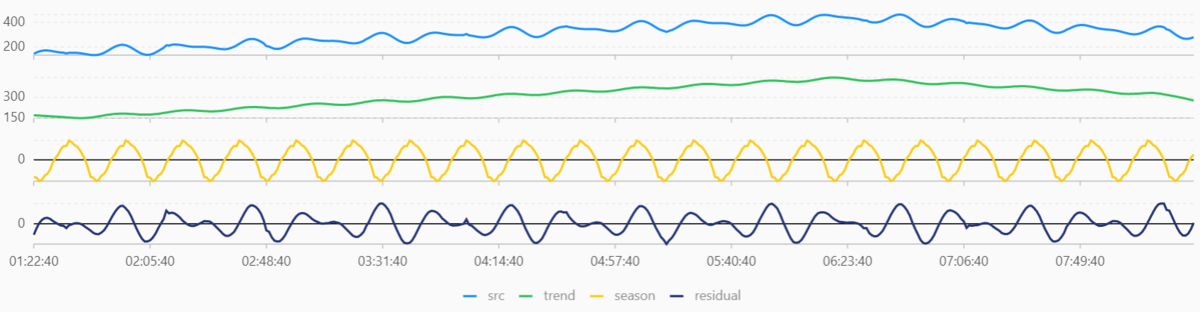
データBと比較すると、 season と residual に大きな変化はありませんが、 trend で上昇と下降の情報がしっかりと出ています。 データBに上昇と下降を付与しただけですので、正しく時系列の分解ができていそうだということがわかりますね。
最後に
今回は、LogServiceで扱えるさまざまな時系列データの処理を行ってみました。
プログラミング等を行わなくても、非常に簡単に時系列データの分析をおこない視覚化してくれる便利な機能ですね。
ただ、データの特性によってそれぞれの関数・パラメータが有効かどうかが異なってくるので、運用する際はまずはじめにどの関数を使うべきかを見極める必要があります。
本ブログでは行いませんでしたが、LogServiceでは使用したクエリをダッシュボードに登録し定期的に更新・閲覧できるようにしたり、時系列分析の結果をもとにアラート設定等を行うなどが可能です。
また、難易度は高いですが PAI と連携し、教師あり学習に発展させるなど高度な機械学習を行うことも可能となります 。
